Fall 2022

Fall 2022 Projects

Machine learning and games Heading link

Chess, etc.

Project Supervisors: Evangelos Kobotis and Drew Shulman

Neural networks have been developed to recognize handwritten text, predict housing prices, improve autonomous driving systems, and even play games like chess and Go.  A neural network is an example of a **machine learning algorithm**.  In this project, we will explore machine learning algorithms and apply them to chess and other games, and data in general.  We will begin with the simplest of games such as tic-tac-toe, and we will try to touch upon more complicated games such as chess. We will use these goals in order to introduce the student to the mathematical treatment of the respective games and to also write concrete programs that will implement the corresponding algorithms. We would like to explore different directions, depending on the students’ preferences, and our hope is to make this a fun project that will serve as an introduction to some modern techniques in computer programming.

The quest for prime numbers Heading link

Escher

Project Supervisor: Evangelos Kobotis

The purpose of this exciting project is to acquaint the student with the mysteries of prime numbers and explore the numerical techniques that allow us to explore them. Our main goal will be to become acquainted with the different primality tests and use them in practice in order to see what it takes to find never-seen-before prime numbers. All theory will be explained in detail.

Prerequisites: An interest in prime numbers. All background material and programming techniques will be covered from scratch.

Poster:   Primality-TestingPoster-Fa22

 

Mathematics of Gerrymandering Heading link

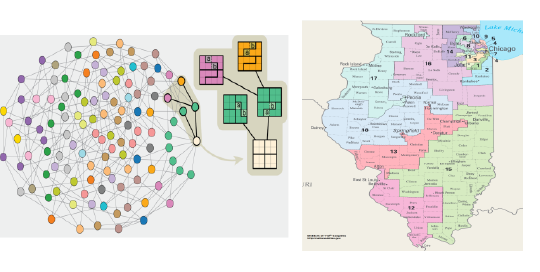
Gerrymandering
Moon Duchin - mggg.org

Project Supervisor: Kevin Whyte

The ways in which voters are divided in districts can dramatically affect the results of elections – amplifying or suppressing the representation of different groups.    However deciding whether a given districting plan is fair is a difficult problem.   For example, adults in Illinois identify themselves as 48% democrat, 33% republican, and 19% with no preference.  The current 18  congressional districts are divided with 13 democratic and 5 republican representatives.  Is that a fair result?  How is it affected by the concentration of voters in Chicago? Does it matter that these are located along the border of the state?    In order to explore such a question we would want to look at predicted election results for a “typical” or “random” district map.  Defining what that means is not so simple, and even in the most basic models there are far too many possible maps to examine all of them.    We will learn about the mathematics of random walks and what different models say about the expected results in various scenarios.

Prerequisites: Some probability/statistics and programming experience would be helpful.

Poster:    GerrymanderingPoster-Fa22

 

Numerical Method for the Heat Equation in 2D Heading link

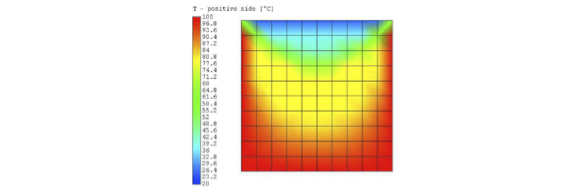
Heat equation

Project Supervisor: Shokouh Pourarian

Laplace’s equation

$\Delta u = 0 \ \ \ \ \left( \frac{\partial^2u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0 \right) $

Arises in the study of steady state or time independent solutions to the two-dimensional heat transfer equation, where u represents temperature. In this project, a numerical technique is implemented on Laplace’s equation to study the heat transfer on a rectangular plate when its walls are subject to constant temperatures (Dirichlet Boundary Conditions). The numerical scheme replaces partial differential equations with a linear system of equations to approximate the temperature distribution throughout the plate given the boundary conditions.

 

Prerequisites: Math 210, Math 220, and programming experience.

Poster:    LaplacePoster-Fa22