Spring 2023
Spring 2023 Projects
Errors-in-variables problems in statistical analysis of random objects Heading link
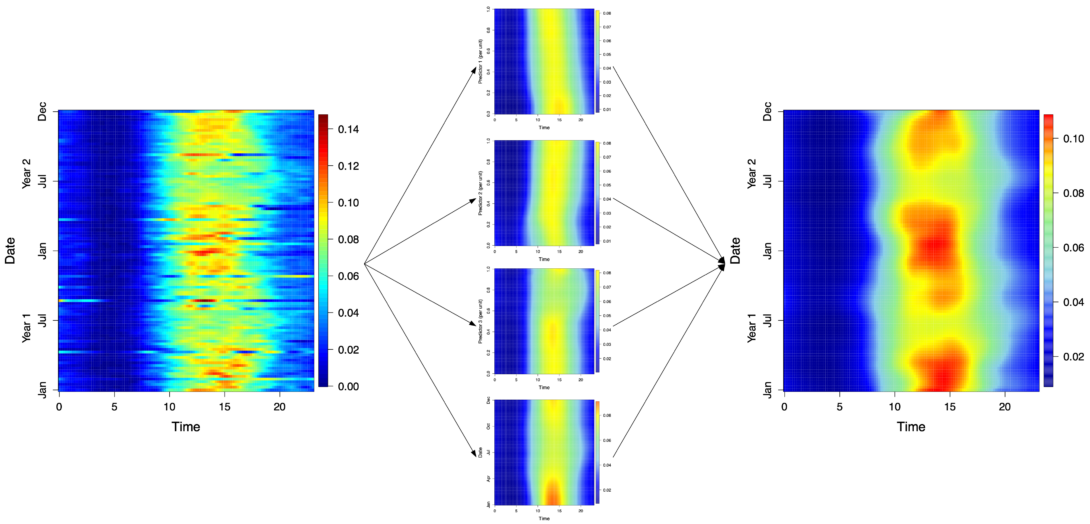
Project Supervisor: Kyunghee Han
Project members: Max Nguyen, Tom Hammons, Xinyu Qin, Jiuhang Qin
In the data science literature, there are growing concerns about the reproducibility of quantitative studies, where statistical inference is misled by unobservable measurement errors or systematic noises in raw data. Even for simple linear regression models, the presence of measurement errors in covariates causes the estimated slope coefficient to be biased toward zero, called attenuation bias, and the situation becomes much worse when we are interested in nonlinear relationships. In this project, we will learn about errors-in-variables problems in statistical analysis of random object analysis that has become an important class of research framework in modern statistics in response to new challenges with the surge of data complexity.
Prerequisites: Probability, statistics, and programming experience would be helpful.
Poster: SIMEXFrechetPoster-Sp23
Machine learning, chess and mathematics Heading link
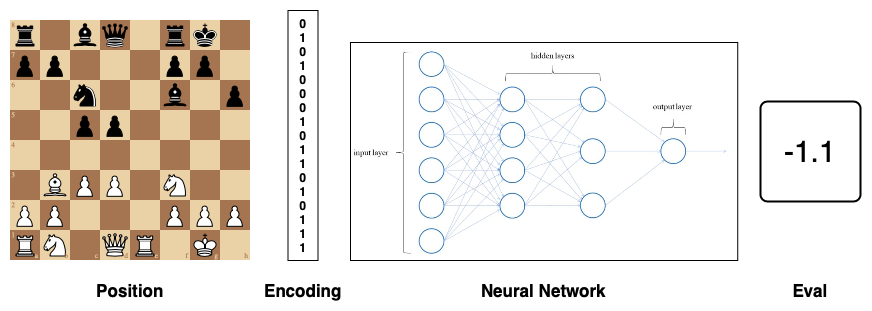
Project Supervisors: Drew Shulman and Evangelos Kobotis
Team members: Zain Aamer, Sravani Bhamidipaty, Nirgun Goel, Bill Shepelak, Xuan Duc Tran, Ling Yu
Neural networks have been developed to recognize handwritten text, predict housing prices, improve autonomous driving systems, and even play games like chess and Go. A neural network is an example of a **machine learning algorithm**. In this project, we will explore machine learning algorithms and apply them to chess. Our goal is to introduce the student to the mathematical treatment of chess and to also write concrete programs that will implement relevant algorithms. Chess and neural networks are two vast fields of study and we would like to explore different directions, depending on the students’ preferences, and our hope is to make this a fun project that will serve as an introduction to some modern techniques in computer programming.
Poster: ChessPoster-Sp23
The quest for prime numbers Heading link
Project Supervisor: Evangelos Kobotis
Team Members: Erick Calderon, Christian Coirin, Hasti Mehta, Savannah Nichols
The purpose of this exciting project is to acquaint the student with the mysteries of prime numbers and explore the numerical techniques that allow us to explore them. Our main goal will be to become acquainted with the different primality tests and use them in practice in order to see what it takes to find never-seen-before prime numbers. All theory will be explained in detail.
Prerequisites: An interest in prime numbers. All background material and programming techniques will be covered from scratch.
Poster: Primality-Testing-Sp23
Computational nonimaging geometric optics: Monge-Ampere Heading link
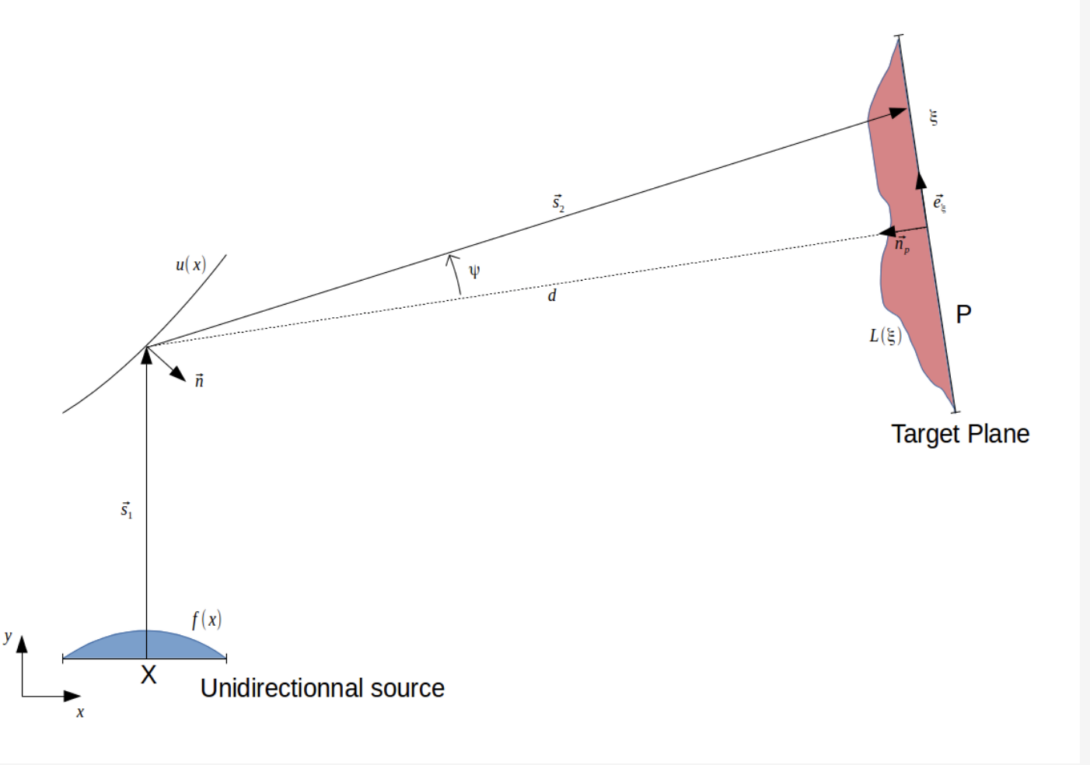
Project Supervisor: Gerard Awanou
Team Members: Kavelle Harlan, Sergio Lara, Amr Mohamed
The design of lenses and mirrors, in free form i.e. with no a priori symmetry assumption, has a long list of applications including materials processing, energy concentrators, medicine, antennas, computing lithography, laser weapons, optical data storage, imaging etc. In this project, we will review in the one dimensional case methods that have been proposed to get numerical approximations. Students will learn latex, Julia, basic numerical analysis, basic linear algebra, and be exposed to the kind of questions researchers address in the numerical analysis of differential equations.
Prerequisites: Math 220 and a basic knowledge of programming.
Poster: Monge-Ampere-Sp23