Spring 2024

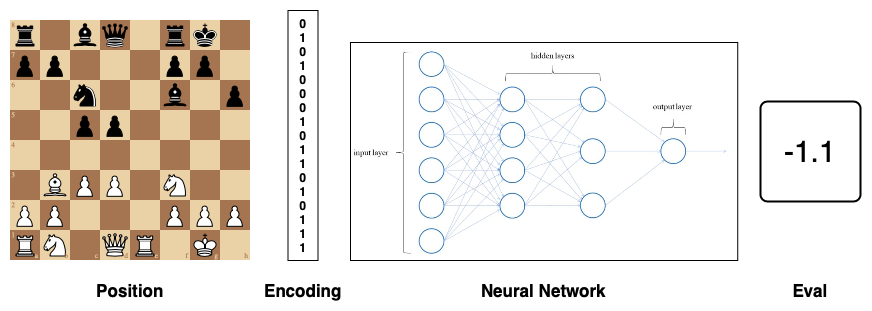
Project Supervisors: Drew Shulman and Evangelos Kobotis

Neural networks have been developed to recognize handwritten text, predict housing prices, improve autonomous driving systems, and even play games like chess and Go.  A neural network is an example of a **machine learning algorithm**.  In this project, we will explore machine learning algorithms and apply them to chess.  Our goal is  to introduce the student to the mathematical treatment of chess and to also write concrete programs that will implement relevant algorithms. Chess and neural networks are two vast fields of study and we  would like to explore different directions, depending on the students’ preferences, and our hope is to make this a fun project that will serve as an introduction to some modern techniques in computer programming.

Project Supervisor: Evangelos Kobotis

The purpose of this exciting project is to acquaint the student with the mysteries of prime numbers and explore the numerical techniques that allow us to explore them. Our main goal will be to become acquainted with the different primality tests and use them in practice in order to see what it takes to find never-seen-before prime numbers. All theory will be explained in detail.

Prerequisites: An interest in prime numbers. All background material and programming techniques will be covered from scratch.

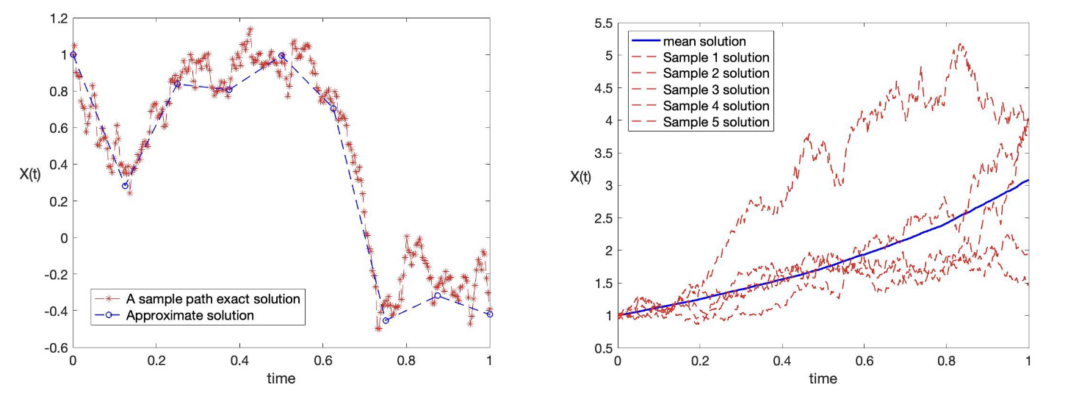
Project Supervisor: Liet Vo

Stochastic differential equations (SDEs) play a very important role in a
range of application areas, including biology, chemistry,
epidemiology, fluid mechanics, microelectronics, economics, and
finance. In general, it is impossible to obtain analytical solutions for
the SDEs due to the nonlinear structure of the noise term. So, solving
the SDEs numerically is the only efficient option. In this project, we
will study how to solve the SDEs by using numerical methods such as
the Euler-Maruyama method and the Milstein method. We will also
learn how to show the rates of convergence for the numerical
solutions theoretically and numerically. A few SDEs will be considered
in this project including the stochastic Black-Scholes equation with
applications in finance, the stochastic Langevin equation, and the
stochastic Hodgkin-Huxley system with applications in biophysics.

Prerequisites: Applied Linear Algebra, Introduction to Probability, ODEs, and MATLAB.

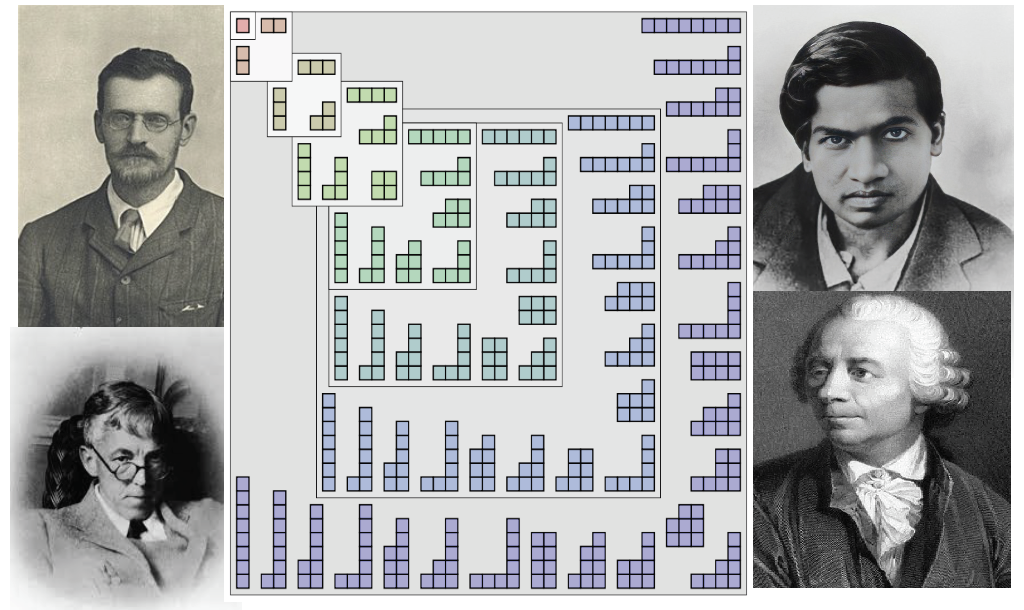
Project Supervisor: Daniel Ingebretson

How many ways are there to sum positive integers to eight? What about if all the summands are odd, or have the same remainder after division by three? These are some questions about integer partitions, a field of additive number theory that Euler started in 1748 and is an active and exciting area of research today, with many connections to other fields of mathematics. In this project we’ll use combinatorial and analytic techniques to study partition identities, equations relating partition quantities. These identities reveal the deep and beautiful additive structure of the integers, and many of these were discovered in  the late 19th and early 20th centuries by Rogers, Ramanujan, Hardy, and others. We’ll use proofs and computer programs to verify some of these partition identities, and search for new ones.

Prerequisites: Math 215 or its equivalent. Some programming experience will be helpful, but is not necessary.

Project supervisor: David Nicholls

Partial Differential Equations (PDEs) are indispensable tools for the modeling of phenomena of physical interest. Typically, useful closed-form solutions are unavailable and one must resort to numerical simulation to discover meaningful quantitative information about solutions. In this Project we will investigate two popular methods for these simulations: The Finite Difference and Finite Element Methods. We will use these to approximate solutions of the three canonical second order linear PDEs: The Wave Equation, the Heat Equation, and Laplace’s Equation.  This will involve both theoretical discussions of accuracy, stability, and convergence, and practical implementations in a high-level computing language.

Prerequisites: Math 210, Math 220, programming experience.