Fall 2024

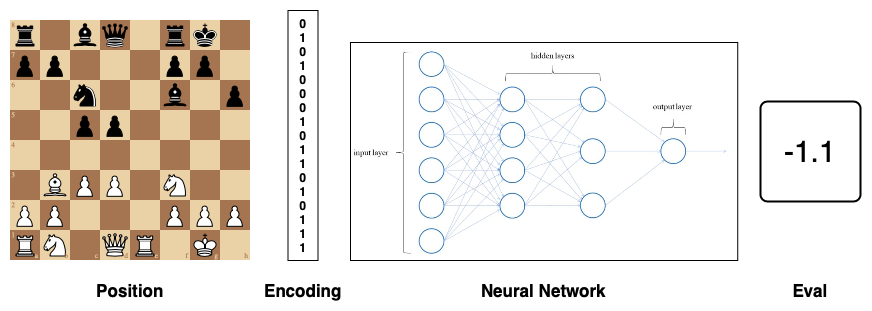
Project Supervisors: Drew Shulman and Evangelos Kobotis

Neural networks have been developed to recognize handwritten text, predict housing prices, improve autonomous driving systems, and even play games like chess and Go.  A neural network is an example of a **machine learning algorithm**.  In this project, we will explore machine learning algorithms and apply them to chess.  Our goal is  to introduce the student to the mathematical treatment of chess and to also write concrete programs that will implement relevant algorithms. Chess and neural networks are two vast fields of study and we  would like to explore different directions, depending on the students’ preferences, and our hope is to make this a fun project that will serve as an introduction to some modern techniques in computer programming.

Project Supervisor: Evangelos Kobotis

The purpose of this exciting project is to acquaint the student with the mysteries of prime numbers and explore the numerical techniques that allow us to explore them. Our main goal will be to become acquainted with the different primality tests and use them in practice in order to see what it takes to find never-seen-before prime numbers. All theory will be explained in detail.

Prerequisites: An interest in prime numbers. All background material and programming techniques will be covered from scratch.

Project Supervisor: Daniel Ingebretson

Any real number $ x $ can be written as its integer part $ \lfloor x \rfloor \in \mathbb{Z} $ plus its fractional part $ \{ x \} \in (0,1) $. How is the sequence $ \{ \sqrt{2} \}, \{ 2 \sqrt{2} \}, \{ 3 \sqrt{2} \}, \ldots, $ distributed in the interval $ [0,1] $? How about the sequence $ \{ \pi \}, \{ \pi^2 \}, \{ \pi^3 \}, \ldots $? The answer to the first question is a well-known theorem of Weyl, and the second is a difficult open problem.

In this project we will study distribution of sequences of this form in the interval, using tools from real analysis, with applications to numerical integration and discrepancy.

Time permitting, we will explore connections with diophantine approximation, dynamics, and ergodic theory.

Prerequisites: Math 215. Some knowledge of real analysis will be helpful but not required.

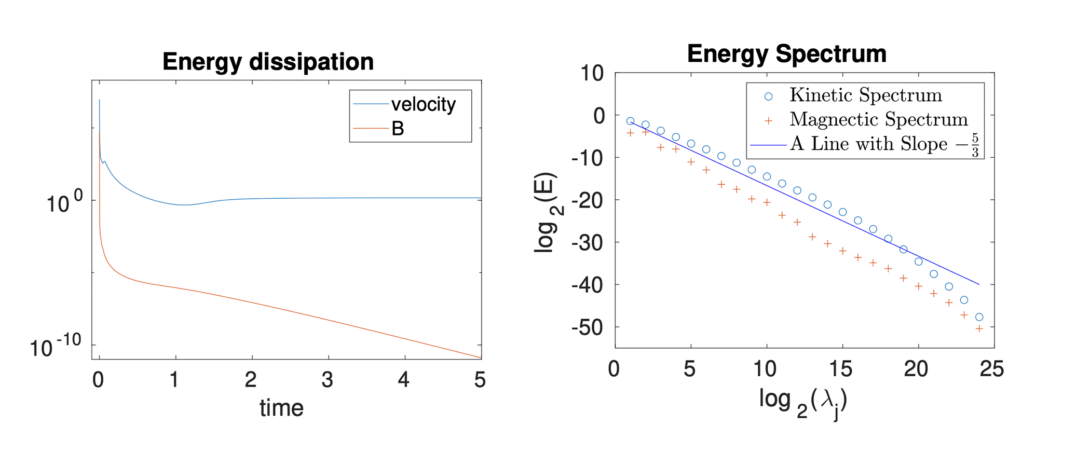
Project supervisor: Mimi Dai

Prerequisites: Math 210, Math 220.

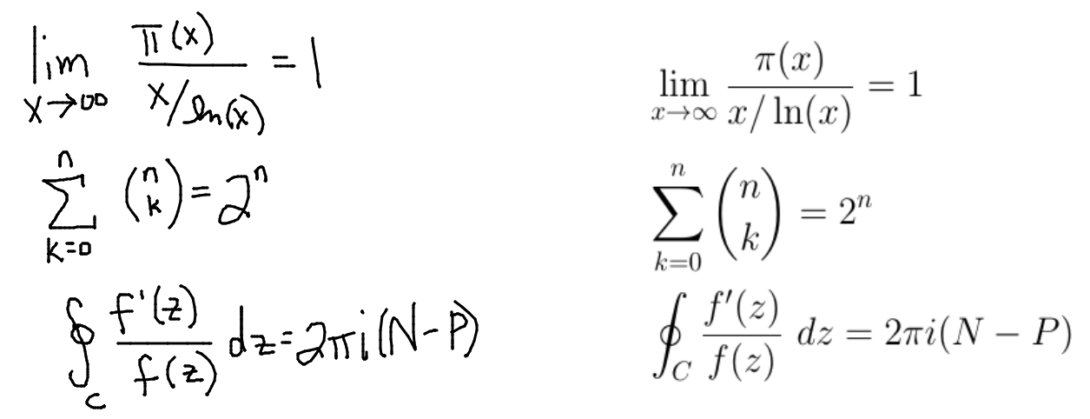
Project Supervisors: Drew Shulman and Evangelos Kobotis

The purpose of this project is to introduce students to Neural Networks in the context of dynamic optical character recognition related to mathematical writing. We will explore how neural networks allow us to recognize handwritten text and turn it into digital text that can be further processed and typeset. We will also try to explore the dynamic side of things with the goal of producing software that will turn mathematical writing dynamically into digital content. The first part of the project will focus on the basics of Neural Networks and mathematical typesetting, whereas the latter and most important part will focus on linking these two items.

Prerequisites: none

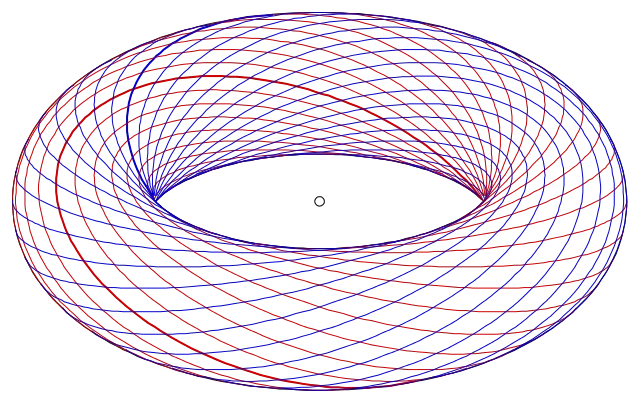
Project Supervisor: Evangelos Kobotis

The purpose of this project is to introduce the student to the magical work of elliptic curves and one of the fascinating problems of their theory. An elliptic curve amounts to considering an equation as simple as $y^2=x^3+ax+b$, with $a$ and $b$ integer numbers. One wants to find all the pairs of rational numbers $(x,y)$ that satisfy this equation. It turns out that one can add such points and generate a group law that in some sense gives a measure of the complexity of the underlying elliptic curves. The understanding of this group of rational points has been an important problem for many years that branches off to all sorts of interesting questions. Our interest will lie in understanding as much as possible about this group and in particular about its rank. No initial knowledge of the field or of programming is required.

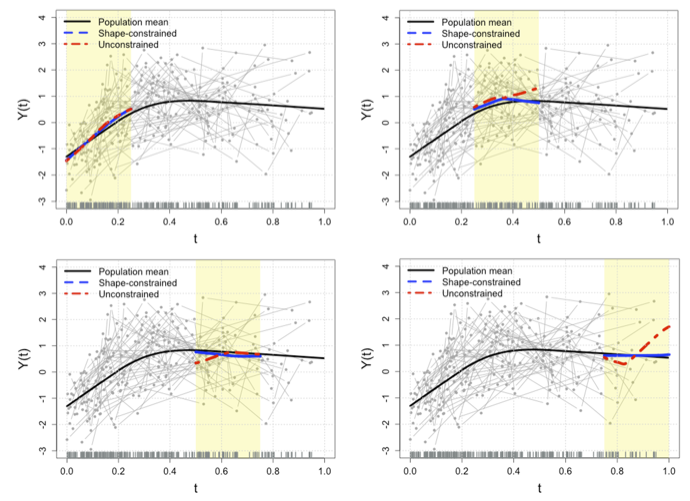
Project Supervisor: Kyunghee Han

The statistical analysis of random objects has become an important class of research framework in modern statistics and machine learning literature. In response to new challenges with the surge of data complexity in data science, data sets that consist of random objects like curves, images, and manifolds are frequently involved. The standard methods in functional data analysis usually assume random objects are fully observed. However, it is more common in practice that responses are partially observed and irregularly collected at subject-dependent times. This often leads to an irregular density of observations, which makes statistical inferences on functional shapes inconsistent per the domain of interest. In this project, shape-constrained functional data analysis will be introduced, and students will have experience in statistical analysis of real data.

Prerequisite: Probability, statistics, and programming experience

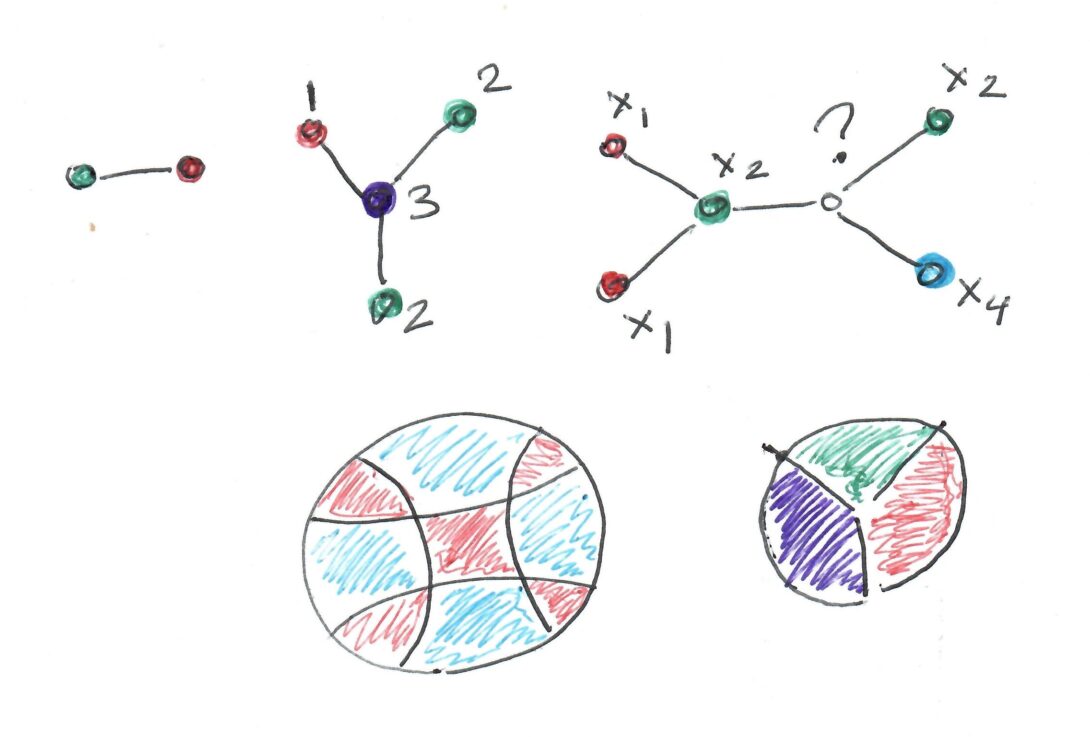
Project Supervisor: Victor Protsak

The idea of coloring is quite old, and also very natural: given a set of objects, some of which are said to be adjacent, assign to each of them a label, or color, in a such a way that adjacent objects are colored differently. One can ask whether colorings exist and how to count them. This has been applied to planar maps, where two regions are adjacent if they share a piece of boundary (Four-Color Problem), and to abstract mathematical graphs, where two vertices are adjacent if they are connected by an edge (chromatic polynomial). In 1995, Richard Stanley has encapsulated all colorings of a finite graph G in its chromatic symmetric function X(G). In spite of extensive research, many fundamental questions remain unsolved (for example, which functions are possible?). The aim of this project is to explore X(G)’s from theoretical and computational perspectives.

Prerequisites: Interest in algebra and combinatorics, Math 215 and CS 151 (or equivalent).  Programming experience with algebraic structures (e.g. in SAGE) would be helpful.