Spring 2022

Spring 2022 Projects

Folding paper from planar tilings Heading link

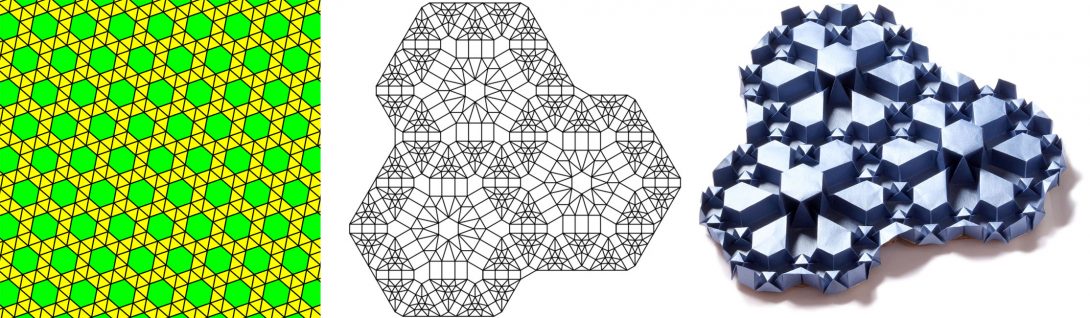
Tiling to folding
Wikipedia, Uyen Nguyen and Ben Fritzson

Project Supervisor: Marcus Michelen

There are many ways to tile the plane using regular polygons.  Tilings for which there are only k different types of vertices are called k-uniform tilings.  The goal of this project is to implement an algorithm that takes in a k-uniform tiling and outputs a crease pattern for folding paper into a pattern inspired by this tiling.  Once the crease pattern is made, they can either be etched onto paper to be folded or fed into an origami simulator to create a 3D model.
Outcomes:  We wrote a program to implement the planned algorithm.  It takes in a “gluing pattern” to describe an arbitrary k-uniform tiling, then plots the tiling, creates the crease pattern according to the algorithm of Nguyen and Fritzson, and outputs it as a .dxf file.  We also implemented the option of coloring mountain and valley folds red and blue so that the folding may be simulated in an online origami simulator.

"Impossible" Behavior: a Mathematical Investigation into Quantum Tunneling Heading link

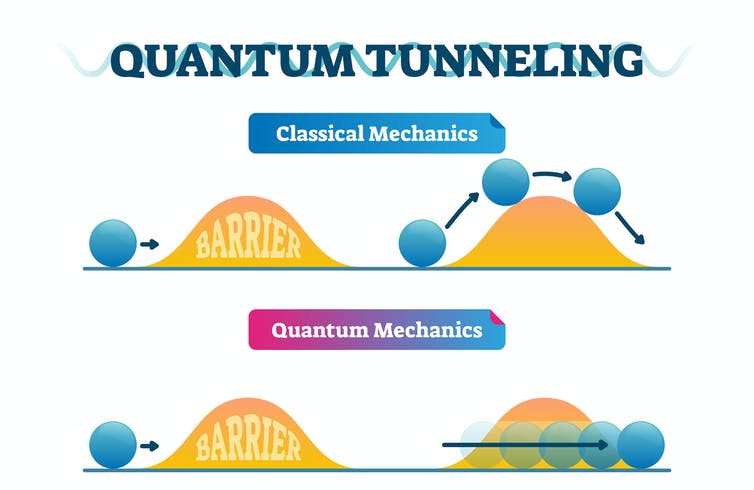
Quantum Tunneling
https://theconversation.com/we-did-a-breakthrough-speed-test-in-quantum-tunnelling-and-heres-why-thats-exciting-113761

Project Supervisor: Evelyn Richman

In classical mechanics, objects obey rigid and intuitive laws of motion; a ball left to roll down a hill will not have enough energy to roll over a second, taller hill. The same behavior might be expected of charged particles (like electrons) in “hills” made of electric potentials. However, the Schrodinger equation, which governs the dynamics of quantum particles, suggests that particles can cross potentials which have more energy than the particles themselves. This phenomenon is known as quantum tunneling. In this project, we will attempt to prove the existence of quantum tunneling by using tools from mathematical analysis and partial differential equations.
Outcomes: By comparing free evolution systems to those with “thin” barrier potentials, we successfully proved that quantum tunneling must occur as the square-integral (also called the L^2 norm) of the barrier potential goes to zero, even if the height of the barrier does not change. We also showed that this must remain true even when arbitrary background potentials are considered, demonstrating that the phenomenon of tunneling is not limited to the well known and explicitly solvable cases. We note however that our results only show that tunneling occurs and provide no estimates on the actual rate of tunneling. Obtaining such estimates could be an interesting task for future research.

Exploring Lattice Polytopes through Problems Inspired by Combinatorial Commutative Algebra Heading link

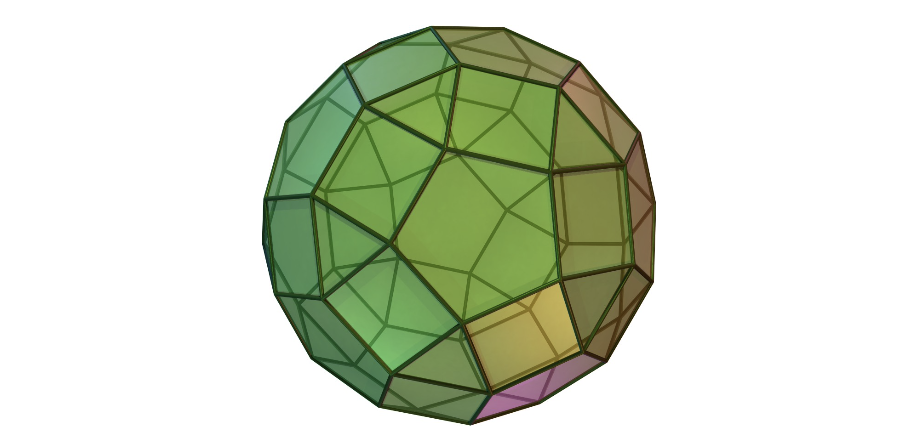
Rhombicosidodecahedron
https://en.wikipedia.org/wiki/File:Rhombicosidodecahedron.jpg

Project Supervisor: Kevin Tucker

Polytopes are higher-dimensional generalizations of two dimensional polygons and three-dimensional polyhedra, and are geometric objects with interesting combinatorial properties. They have applications to diverse areas of both pure and applied mathematics, and in particular are used to study toric varieties in algebraic geometry and affine semi-group rings in commutative algebra.  The geometry of polytopes is particularly well-suited to experimentation, and there is indeed much to explore as a number of easy to formulate and long-studied questions about polytopes remain unanswered. In this project, we will leverage the connection between algebra and geometry to explore certain newly defined invariants for affine toric varieties and semi-group rings over finite fields using polyhedral geometry.

Outcomes: We approached computations of dual F-signatures of affine semigroup rings, a numerical invariant of singularities in positive characteristic commutative algebra where a toric description has recently been given. We used the open source software polymake to assist in determining this invariant for the semigroup rings given by various rational polyhedral cones over polytopes. In particular, we investigated the conjectured formula for the dual F-signature of the Veronese subrings of polynomial rings over fields of prime characteristic p > 0. We found that polymake can be a highly effective tool for computations in polyhedral geometry. In particular, it can be used to explore invariants such as the dual F-signature of affine semigroup rings and allows one to make and test formulas such as the conjectured value of the dual F-signature of Veronese subrings. However, computational complexity in the computations required for the dual F-signature may prove to be prohibitive in practice as we increase scale or dimension. We produced several examples demonstrating this barrier where we found that our hardware was insufficient. Looking forward, proving the conjectured formula for the dual F-signature requires a combinatorial approach.

Poster:  InvariantofSemigroupRings.pdf

 

Arboreal dynamics and symmetries in the roots of polynomials Heading link

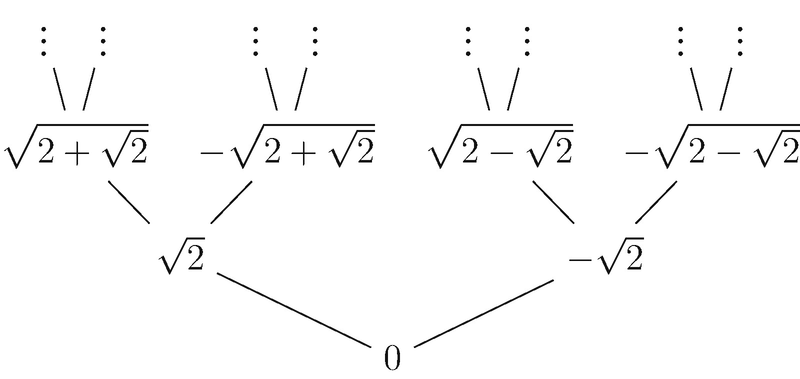
Rooted tree of roots

Project Supervisor: Wouter Van Limbeek

Let f be a polynomial, fix some scalar a, and consider the roots of f^n(x) = a as n tends to infinity. It turns out that all the solutions together form a graph called a “rooted tree” and f induces a map on this graph that pushes vertices towards the root (see picture). For fixed n, there are more symmetries coming from the so-called “Galois group” of f^n and these permute the numbers at a fixed distance from the root. It is conjectured that (aside from some sporadic exceptions) all possible permutations arise, i.e. the roots are “maximally symmetric”. Likewise there is a conjecture characterizing the supposedly very special polynomials that give rise to “minimally symmetric” roots. There is a lot of evidence for these conjectures, but nevertheless they remain open for most polynomials. In this project we will make computer-assisted computations to investigate unknown cases of these conjectures.

 

Outcomes: An interesting observation is that even values of r give us a Galois group with rank 1, prime and prime power values of r give a rank of 1 or 2, and r values that are a product of 2 and a prime power give us a Galois group of rank 2. This pattern has been observed through r=32. Thus, we propose the existence of a correlation between the primality of r and the value of the rank of the Galois group. Given more computational power, a stronger conjecture about the nature of the Galois groups of such polynomials can be made.

 

Poster: ArborealDynamics.pdf

 

Numerical adventures with prime numbers Heading link

Escher
"Day and Night" by Escher

Project Supervisor: Evangelos Kobotis

The purpose of this project is to acquaint the student with the mysteries of prime numbers and explore the numerical techniques that allow us to explore them. We will look at numerical questions concerning the distribution of prime numbers, primality testing, sequences of prime numbers and other topics. Our main research goal will be to provide individual prime numbers or sets of prime numbers with interesting properties as well as relevant visualizations For our programs we will mostly use the Python programming language. There will be in person meetings but the project team will meet mostly online

 

Outcomes: During the semester-long project, we explored the properties of prime numbers from scratch. We established an initial range over which we studied patterns, special types of primes and numerically verified fundamental theorems. Then we proceeded beyond this range and examined what it takes to find new (never seen before) prime numbers. Finally we explored some possible graphical representations of prime numbers.

 

Poster: AdventuresPrimes.pdf