Spring 2025
Spring 2025 Projects
Machine learning, chess and mathematics
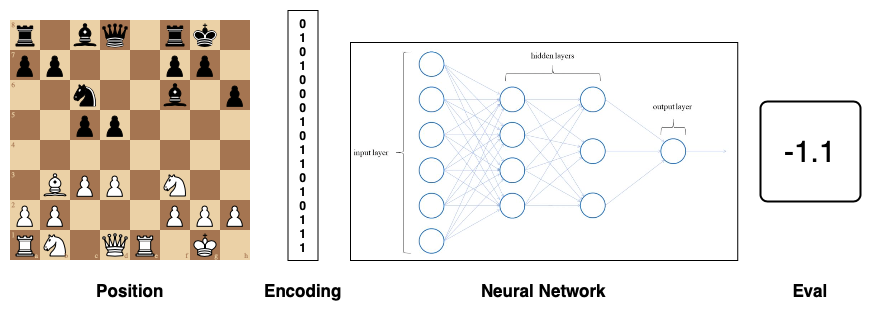
Project Supervisors: Drew Shulman and Evangelos Kobotis
Neural networks have been developed to recognize handwritten text, predict housing prices, improve autonomous driving systems, and even play games like chess and Go. A neural network is an example of a **machine learning algorithm**. In this project, we will explore machine learning algorithms and apply them to chess. Our goal is to introduce the student to the mathematical treatment of chess and to also write concrete programs that will implement relevant algorithms. Chess and neural networks are two vast fields of study and we would like to explore different directions, depending on the students’ preferences, and our hope is to make this a fun project that will serve as an introduction to some modern techniques in computer programming.
The quest for prime numbers
Project Supervisor: Evangelos Kobotis
The purpose of this exciting project is to acquaint the student with the mysteries of prime numbers and explore the numerical techniques that allow us to explore them. Our main goal will be to become acquainted with the different primality tests and use them in practice in order to see what it takes to find never-seen-before prime numbers. All theory will be explained in detail.
Prerequisites: An interest in prime numbers. All background material and programming techniques will be covered from scratch.
Continued Fractions
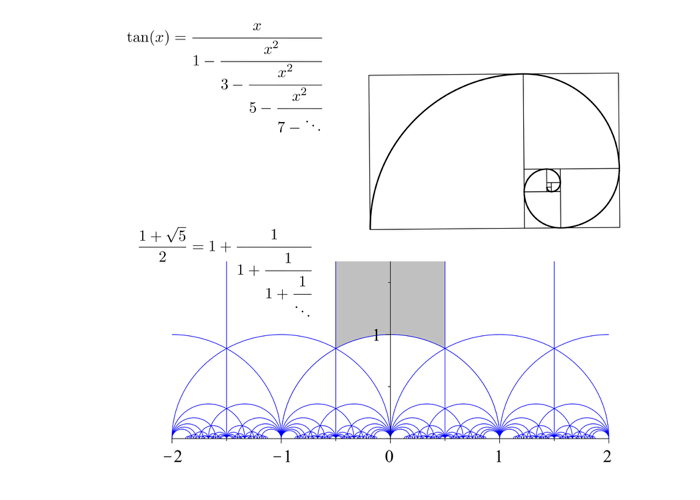
Project Supervisor: Daniel Ingebretson
Prerequisites: Math 215.
Turning handwriting into digital information – the magic of neural networks
Project Supervisors: Drew Shulman and Evangelos Kobotis
The purpose of this project is to introduce students to Neural Networks in the context of dynamic optical character recognition related to mathematical writing. We will explore how neural networks allow us to recognize handwritten text and turn it into digital text that can be further processed and typeset. We will also try to explore the dynamic side of things with the goal of producing software that will turn mathematical writing dynamically into digital content. The first part of the project will focus on the basics of Neural Networks and mathematical typesetting, whereas the latter and most important part will focus on linking these two items.
Prerequisites: none
Rational points on elliptic curves
Project Supervisor: Evangelos Kobotis
The purpose of this project is to introduce the student to the magical work of elliptic curves and one of the fascinating problems of their theory. An elliptic curve amounts to considering an equation as simple as $y^2=x^3+ax+b$, with $a$ and $b$ integer numbers. One wants to find all the pairs of rational numbers $(x,y)$ that satisfy this equation. It turns out that one can add such points and generate a group law that in some sense gives a measure of the complexity of the underlying elliptic curves. The understanding of this group of rational points has been an important problem for many years that branches off to all sorts of interesting questions. Our interest will lie in understanding as much as possible about this group and in particular about its rank. No initial knowledge of the field or of programming is required.
Exploring Tropical Geometry
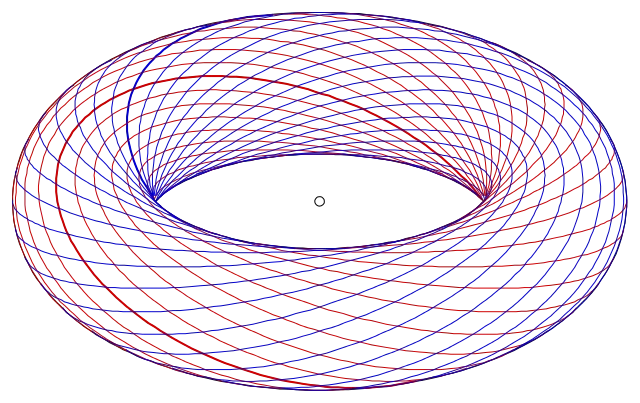
Map Colorings
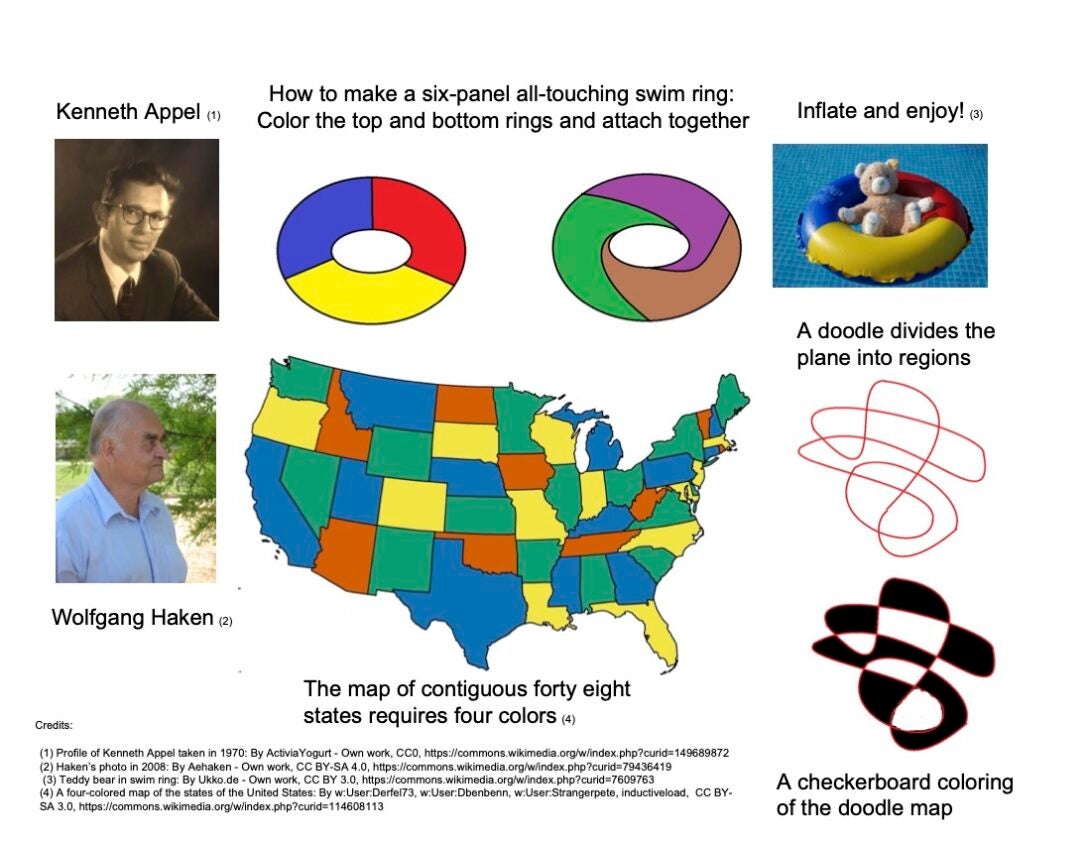
How many colors are needed to properly color a map? And why do some maps require more colors than others? The celebrated Four-Color Theorem asserts that in the plane, four colors always suffice! That is, given several connected regions in the plane (or even on the surface of a sphere) separated by borders, each region can be assigned one of only FOUR colors in such a way that any two regions sharing a common piece of boundary are colored DIFFERENTLY. While the Four-Color Theorem itself was notoriously difficult to prove, requiring an elaborate strategy and extensive computer calculations, many versions of these questions are more accessible. For example, every planar “doodle’’ creates a map that can be colored with only TWO colors! In another direction, if we are bold enough to leave the spherical Earth behind, four colors may not be enough: one can draw seven regions on the surface of a swim ring (torus) that pairwise border each other, thus necessitating SEVEN colors. An easier case of six such regions is illustrated in the picture above. Our goal is to explore the abstract algebra and combinatorics behind map colorings.
Prerequisites: First and foremost, desire to explore unfamiliar mathematical structures without fear or regret. Geometric imagination, as well as Interest in abstract algebra and combinatorics (e.g. familiarity with graph theory and quaternions) would be helpful, but not strictly required.